자극의 전달 문제 연습하기 3편입니다.
[2편 바로가기]
[고등생명과학1] 자극의 전달 문제 연습하기 2편 : 한걸음씩 천천히
자극의 전달 문제 연습하기 2편입니다. [1편 바로가기] [고등생명과학1] 자극의 전달 문제 연습하기 1편 : 같이 도전해봅시다자극의 전달 문제 연습하기 1편입니다. .. 자극의 전달 문제에서는 '결
juningscience.tistory.com
.
.

[시작] 자극을 주고 경과된 시간은 5ms 이므로 자극 지점의 막전위는 -70이 되어야만 합니다.

그러므로 자극지점은 d2만 가능하겠습니다.
또한 신경 I의 막전위를 보면 자극지점으로부터 ㉮ => ㉯ => ㉰ 순으로 막전위가 나와야 합니다.
따라서 ㉮는 -80이고 ㉯는 +30이며 ㉰는 -60이 되어야 합니다.
d4와 d5는 3cm 간격이므로 신경 I의 전도속도는 3cm/ms 입니다.
.
신경 II의 d1 지점은 막전위가 -80 입니다.
d2에서 d1 까지 이동하는 데에 2ms가 소모되어야 하므로 ⓐ는 2cm가 되겠습니다.
.
위 문제의 답은 ㄱ, ㄴ, ㄷ 입니다.

[코멘트] 자극지점을 안다면 자극지점으로부터 멀어질수록
어떤 막전위가 나오게 되는 지 경향성을 주목해보세요.
.
.

[시작] 신경 III의 t2 자료를 집중해봅시다.
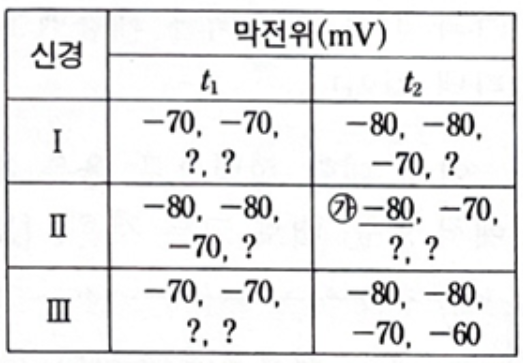
-80이 두 지점에서 나와야 하므로 자극 지점 Q는 d2, d3 중 하나입니다.
.
가정 : t2가 5ms 라면?
신경 III의 전도 속도는 1cm/ms가 되어야 합니다.
그래야 -80이 두 지점에서 나올 수 있기 때문입니다.
신경 II의 t1(4ms) 자료를 보면 두 지점에서 -80이 나와야 합니다.
그러므로 신경 II의 전도 속도는 2cm/ms 이며 자극지점 P는 d2, d3 중 하나입니다.
신경 I의 t2(5ms) 자료를 보면 두 지점에서 -80이 나와야 합니다.
신경 I의 전도 속도는 1cm/ms 가 되어야 하고 자극지점 P는 d3가 되어야 하겠습니다.
자극지점 Q는 P와 달라야 하므로 d2가 됩니다.
.
위 문제의 답은 ㄴ, ㄷ 입니다.
.
.

[시작] X에 자극을 주었을 때 (가) 신경 막전위에 주목해봅시다.
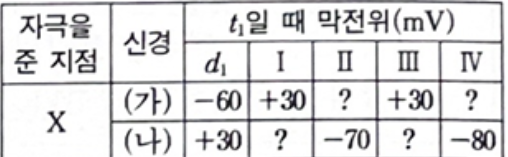
d2~d5 중에 +30 막전위인 곳이 2곳입니다.
신경 A에서는 불가능하므로 신경(가)는 B에 대응됩니다.
또한 자극을 준 지점 X가 d3여야 2곳에서 +30이 나올 수 있겠습니다.
신경B는 d1에서 막전위가 -60이고 신경A는 d1에서 +30입니다.
그러므로 신경B의 전도 속도는 2cm/ms이고 신경A의 전도 속도는 3cm/ms 입니다.
또한 t1은 4ms가 되겠습니다.
.

자극 지점이 Y일때 신경B의 d1지점은 막전위가 -80 입니다.
그러므로 Y는 d2가 되겠습니다.
만약 I이 d2였다면 신경A에서 막전위가 +30이 나올 수 없으므로 I은 d4가 되겠습니다.
.
위 문제의 답은 ㄱ 입니다.
.
.
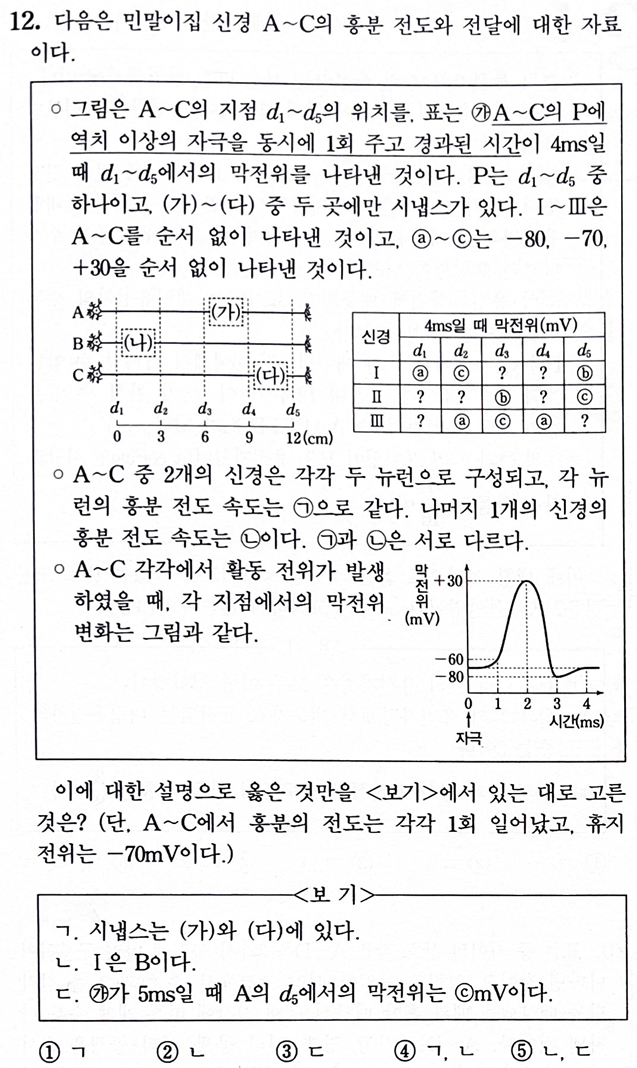
[시작] 자극후 경과한 시간은 4ms이므로
자극 지점의 막전위는 무조건 -70이여야 합니다.
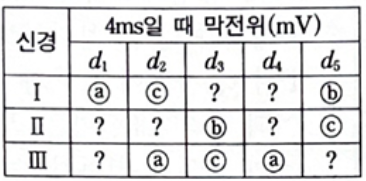
자극지점은 신경 I, II, III 에서 모두 -70이여야 하므로 d1, d4 중 하나가 자극지점이 되겠습니다.
자연스럽게 ⓐ는 -70이여야 합니다.
가정 : d4가 자극지점이라면?
신경 III을 보면 d2의 막전위가 -70이고 d3의 막전위가 ⓒ입니다.
만약 ⓒ가 -80이라면 만족하는 신경이 없으므로 ⓒ는 +30이여야 합니다.
또한 모든 신경에서 d4 앞쪽으로 막전위가 ⓑ이거나 ⓒ인 지점이 있으므로
(가)에는 시냅스가 있으면 안됩니다.
그러므로 (나)와 (다)에 시냅스가 있습니다.
신경 B와 C는 전도 속도가 같으므로 d2, d3, d4의 막전위가 모두 같아야 합니다.
그러므로 신경 III이 신경 A가 되겠습니다.
신경 I은 d5 막전위가 -80이고 신경 II는 d5 막전위가 +30 입니다.
따라서 신경 I이 신경 B이고 신경 II가 신경 C에 대응되겠습니다.
.
위 문제의 답은 ㄴ 입니다.
'생명과학1 해설 저장소 > 기타 자료 해설' 카테고리의 다른 글
| [고등생명과학1] 유전 문제 연습하기 13편 : 최대한 파헤친 후 가정하자 (0) | 2024.11.09 |
|---|---|
| [고등생명과학1] 근수축 문제 연습하기 5편 : 처음보는 자료라도 본질에 충실하면 됩니다 (0) | 2024.11.02 |
| [고등생명과학1] 자극의 전달 문제 연습하기 2편 : 한걸음씩 천천히 (0) | 2024.10.26 |
| 생명과학1 - 자극의 전달 문제 연습하기 1편 : 자료 분석 하기 (0) | 2024.10.25 |
| [고등생명과학1] 근수축 문제 연습하기 4편 : 한 시점의 모든 길이 구하는 것을 목표로 삼자 (0) | 2024.10.24 |



