이번 게시물은 근수축 문제 연습하기 2편 입니다.
[1편 바로가기]
[고등생명과학1] 근수축 문제 연습하기 1편 : 길이 변화량을 문자로 잡자
이번 게시물은 근수축 문제 연습하기 1편 입니다. .. 현재 (2024) 시점에서 보았을 때 근수축 문제의 트렌드는 길이의 차를 자료로서 많이 줍니다. 이럴때는 길이의 변화량을 문자로 잡아 생
juningscience.tistory.com
.
.
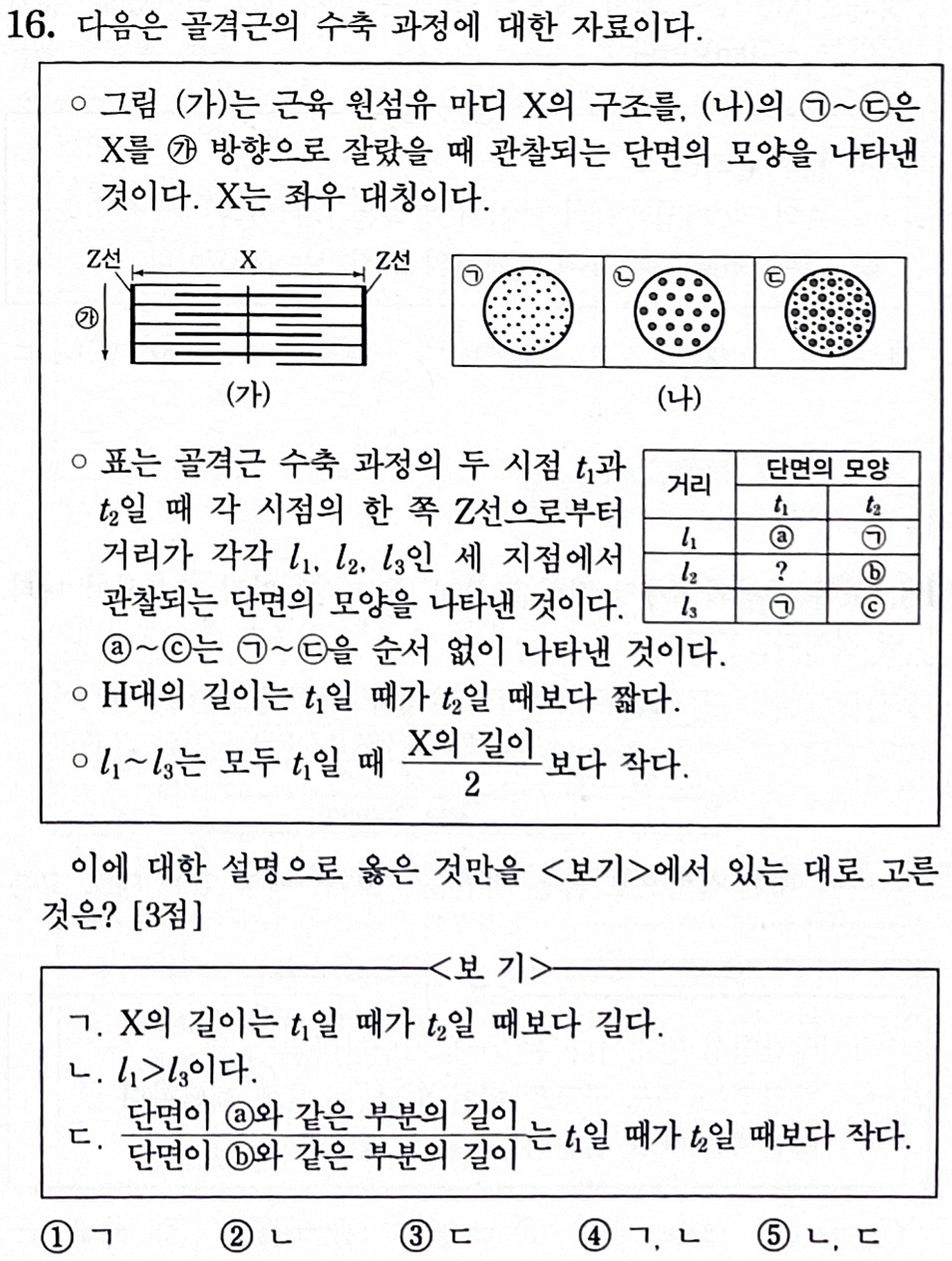
[시작] 불변의 진리가 있습니다.
"㉡부분에 닿을 수 있는 길이라면 영원히 ㉡에 닿는다."
그러므로 ⓐ와 ⓒ는 ㉡이 될 수 없으므로 ⓑ가 ㉡입니다.
.
우선 문제의 조건에 의해 t2에서 t1 보다 X의 길이가 더 깁니다.
그러므로 ⓒ가 ㉠이여야만 합니다.
.
위 문제의 답은 ㄴ 입니다.
.
.

[시작] (가)에서 ⓐ는 ㉠ 입니다.
.
가정 : ⓑ를 ㉡이라고 해봅시다.
t1에서 t2가 될때 X가 0.8 감소하고 ㉡이 0.4 증가하면 됩니다.
그러면 ㉠ - ㉢ 값이 t1에서 t2가 될때 0.2 감소할 수 없으므로 모순입니다.
.
가정 : ⓑ를 ㉢ 이라고 해봅시다.
X가 0.2 감소하고 ㉢이 0.2 감소하면 되겠습니다.
㉠ - ㉡ 값은 0.2 감소하므로 맞는 가정입니다.
.
t1에서 X + ㉢ 의 길이가 4.4 입니다.
이때 ㉠ + ㉡의 길이가 1이므로 4.4 - 2 = 2.4 는 2㉢ 길이와 같습니다.
t1에서 ㉢의 길이는 1.2 입니다.
㉠ - ㉡ 값은 0.6이므로 ㉠ + ㉡ = 1 식과 연립하면
㉠은 0.8이고 ㉡은 0.2 입니다.
.
위 문제의 답은 ㄱ 입니다.
.
.

[시작] 문제 시작에 앞서, 주의할 점이 있다면 ㉢이 H대 길이의 절반이라는 점입니다.
문제의 자료에 의해 t1에서 t2로 갈때 X의 길이는 0.8 증가했습니다.
또하나의 식이 있다면 t1에서 ㉠ + ㉡ + ㉢ = 1.2 입니다.

위 자료에서 ㉡ 길이를 3이라고 놓아봅시다.
㉠ + ㉡ + ㉢ = 1.2
에서 ㉠, ㉡, ㉢ 이 모두 소수점 한자리로 나누어 떨어지려면
㉡ 길이를 3이라고 할때, ㉠ + ㉢ 길이는 1이거나 3 이여야 합니다.
가정 : ㉠ + ㉢ 길이가 3이라고 해봅시다.
㉠ - ㉢ = 1 이므로 ㉠은 2이고 ㉢은 1입니다.
㉠ + ㉡ + ㉢ = 6 인데 실제값은 1.2 이므로 모든 값에 0.2를 곱하면 실제값으로 변환가능합니다.
㉠ = 0.4, ㉡ = 0.6, ㉢ = 0.2 입니다.
그러므로 t2에서 ㉠ = 0.8, ㉡ = 0.2, ㉢ = 0.6 입니다.
문제의 맨 마지막 조건에서 M선에서 d1 까지의 거리가 1.1 입니다.
이를 식으로 표현해보면 ㉢ + (㉠ + ㉡) / 2 = 1.1 입니다.
조건을 만족하므로 가정에 이상이 없겠습니다.
.
위 문제의 답은 ㄱ, ㄷ 입니다.

[코멘트] 어차피 실제 시험에서는 복잡한 연립을 통해 길이를 구할 수 없습니다.
시간이 부족하기 때문이죠.
계산을 최소화하는 방법을 고민해야 합니다.
'생명과학1 해설 저장소 > 기타 자료 해설' 카테고리의 다른 글
| [고등생명과학1] 유전 문제 연습하기 7편 : 세포 매칭 문제에서 떠올려야 하는 점은? (0) | 2024.10.13 |
|---|---|
| [고등생명과학1] 유전 문제 연습하기 6편 : DNA 상대량이 4인 유전자? (0) | 2024.10.12 |
| [고등생명과학1] 근수축 문제 연습하기 1편 : 길이 변화량을 문자로 잡자 (0) | 2024.10.12 |
| [고등생명과학1] 유전 문제 연습하기 5편 : 신박한 다인자 유전 문제? (0) | 2024.10.11 |
| [고등생명과학1] 유전 문제 연습하기 4편 : 모르는 개념이 있어서 안풀리는게 아니다 (0) | 2024.10.11 |



